Введение
Для обеспечения своей конкурентоспособности в настоящее время многие машиностроительные предприятия внедряют системы бережливого производства (Lean Production/ Принципы систем бережливого производства основываются на методах формирования потока создания ценности, а также на японской философии «кайдзен» (непрерывного совершенствования). Под потоком создания ценности в бережливом производстве понимают производственный процесс изготовления изделия. При формировании потока создания ценности необходимо устранять и минимизировать все действия, не добавляющие ценности. Ценность - это полезные свойства продукта с точки зрения потребителя, а действия, добавляющие ценность - это любые действия, которые в процессе трансформации сырья в готовый продукт увеличивают его привлекательность и полезность для потребителя [1]. В условиях бережливого производства (при формировании потока или оптимизации технологического маршрута) необходимо реорганизовывать многие производственные подразделения на основе разработки оптимальных технологических планировок оборудования, минимизирующих грузопоток (G) и производственные площади (F). Например, опыт зарубежных авиадвигателестроительных предприятий (Pratt & Whitney, США) по оптимизации производства показал [1], что за время выполнения проекта удалось переместить на другое место все семь тысяч станков, организовать производство двигателей в непрерывном потоке. Поток двигался через производственные модули и попадал на окончательную сборку при помощи простой «вытягивающей системы».
В модулях, где изготовлялись компоненты авиационного двигателя, была произведена реорганизация восьмидесяти бизнес-единиц, каждая из которых отвечала за производство определенной группы деталей. Сказанное позволило Pratt & Whitney уменьшить производственные площади с 12,5 млн кв. футов до 8 млн кв. футов.
Таким образом, можно утверждать, что использование методов математического моделирования и оптимизации технологических планировок оборудования при создании (реконструкции, реструктуризации) производственных цехов бережливого производства на основе рационализации технологических планировок оборудования относится к наиболее актуальным задачам технологической подготовки бережливого производства в машиностроении.
1. Разработка метода искусственного интеллекта для оптимизации планировок оборудования бережливого производства
Задача оптимизации планировок оборудования относится к AP-полным задачам, при решении которых точными методами оптимизации время сходимости алгоритма экспоненциально увеличивается в зависимости от количества единиц размещаемых объектов. На крупных предприятиях количество перемещаемого технологического оборудования, как выше уже было отмечено, измеряется тысячами, а комбинации возможного относительного расположения оборудования измеряется числами, которые находятся за пределами вычислительных возможностей даже супер-ЭВМ. Поэтому решение рассматриваемой задачи предлагается искать с использованием методов искусственного интеллекта, которые за счет распараллеливания вычислительного процесса и поиска локальных оптимумов, позволяют резко сокращать время вычислений на ЭВМ и осуществлять не только однокритериальную, но и многокритериальную оптимизацию технологических планировок оборудования.
В настоящее время известны различные методы искусственного интеллекта для оптимизации размещения оборудования по одному критерию - минимума грузопотока, например, с помощью искусственной нейронной сети Хопфилда [5] и с помощью генетических алгоритмов [2]. Рассматриваемая задача, как выше было отмечено, относится к многокритериальным, что предполагает разработку специальных логико-генетических методов и алгоритмов для определения Парето-оптимальных решений.
Генетические алгоритмы, которые предложено использовать для решения данной задачи, - это процедуры поиска, основанные на механизмах естественного отбора и наследования [3]. В них используется эволюционный принцип выживания наиболее приспособленных особей (в данном случае объектов технологической планировки цеха «бережливого производства»).
Наиболее приспособленные особи (варианты объекта проектирования) получают возможность «воспроизводить» потомство с помощью скрещивания (кроссовера) с другими особями (вариантами объекта) популяции. В генах популяции особей (объектов) могут происходить мутации - стохастические изменения части хромосомы.
Скрещивание наиболее приспособленных особей приводит к тому, что появляются для исследования новые перспективные области из пространства поиска решений задачи. В конечном итоге многошаговая модификация популяций обеспечивает сходимость генетического алгоритма к Парето-оптимальному решению задачи. На основании вышеизложенного предлагается новый метод двухкритериальной оптимизации планировок оборудования, как по критерию минимумов грузопотока, так и величины площади. Для решения задачи оптимизации технологических планировок оборудования была использована система математического моделирования MatLab 7.3.0.
В качестве исходной информации для компьютерного моделирования необходимо задавать: маршруты обработки деталей (по маршрутной карте проектного технологического процесса - ПТП) в виде последовательности номеров станков; массу каждой детали-представителя и программу выпуска. Вначале для укрупненного моделирования и поиска Па-рето-оптимального решения задачи станки можно обозначить в виде прямоугольников, со сторонами, соответствующими их наибольшим габаритам:
w = (w1, w2, ..., wi, ..., wm) - вектор ширины станков;
l = (l1, l2,.,li,., lm) - вектор длины станков и указанием n - количества устанавливаемых станков.
Ограничениями решения задачи являются размеры участка:
W - ширина участка;
L - длина участка.
Для решения задачи также вводится прямоугольная система координат XOY, у которой оси OX и OY в рассмотренном ниже случае совпадают соответственно с верхним левым углом участка или растра (сетки колонн) производственного корпуса.
Набор элементов <l, w> называется допустимой планировкой, если выполнены следующие условия:
1) прямоугольники не перекрывают друг друга;
2) прямоугольники не выходят за границы участка:
n n
W > Z wi ; L > Z li ,
i=i i=i
где n - количество устанавливаемых станков.
При выполнении условий допустимости требуется найти такую планировку оборудования, для которой и суммарный грузопоток (ZGi), и производственная площадь (F) стремятся к минимуму. При этом:
D Oi
SGi = ZZ Ni ■ m ■ sij,
i =1 j=1
где Ni - приведенная программа выпуска i-й детали, mi - масса i-й заготовки после j-й операции; sij - длина пути перемещения i-й заготовки после j-й операции; D - номенклатура деталей производственного участка; Oi - количество операций в технологическом процессе изготовления i-й детали-представителя группы.
На этапе формирования начальной популяции хромосомы создают случайным образом как комбинации чисел от 1 до n, где n - количество расставляемых станков. Каждая хромосома представляет собой возможный вариант взаимного расположения оборудования на производственном участке.
Оценивание приспособленности хромосомы в популяции состоит в расчете функции приспособленности (целевой функции), т. е. в расчете нормированного методами многокритериальной оптимизации значения суммарного грузопотока (G) и занимаемой площади (F). Целевая функция рассчитывается как свертка этих критериев:
Ф = axG* +a2F* ® min, (1)
где G*, F* - значения соответственно грузопотока и площади, приведенные к относительному безразмерному виду по следующей формуле [4]:
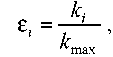
где ki - значение критерия оптимизации на i-й итерации алгоритма, kmax - максимальное значение этого же критерия (в данном случае грузопотока G и площади F); а1, а2 - положительные числа, характеризующие относительную важность критериев оптимизации (G,F): а1 + а2 = 1.
Селекция хромосом производится методом рулетки [3]. Колесо рулетки содержит по одному сектору для каждой особи (варианта объекта), размер которого пропорционален соответствующей величине функции приспособленности. Поэтому чем больше значение функции приспособленности, тем больше сектор на колесе рулетки и вероятность выбора данной хромосомы в качестве родителя.
В данном алгоритме используется двухточечный кроссовер, отличающийся от стандартного тем, что в данном случае в качестве родителя выступает только одна хромосома, в которой случайным образом выбирается две точки разрыва и имеет место обратный порядок записи генов в этом интервале. В результате работы кроссовера получается один потомок.
Условие остановки работы алгоритма имеет два варианта. Первый вариант остановки алгоритма - достижение ожидаемого Парето-оптимального значения, т. е. полученная хромосома является наиболее приспособленной из всей популяции. Второй вариант - выполнение заданного количества итерации (поколений) или шагов расчета.
Решение задачи представляется в виде Па-рето-оптимальной хромосомы, генами которой являются номера станков, а также строится схема расположения этих станков в пространстве цеха (рис. 1).
Оптимальная планировка оборудования (после рассмотренного выше укрупненного математического моделирования с использованием генетического алгоритма многокритериальной оптимизации) разрабатывается на втором этапе, где на основе полученного с помощью логикогенетического метода Парето-оптимального укрупненного макета участка цеха для последующей разработки чертежа технологической планировки оборудования используется темплетный метод макетирования [5].
2. Результаты применения логико-генетического метода оптимизации технологических планировок оборудования
Опытно-технологические работы по практическому использованию предложенного логико-генетического метода многокритериальной оптимизации были произведены на производственных участках механосборочного цеха моторостроительного предприятия. Исходной информацией для компьютерного моделирования послужили имеющаяся технологическая планировка цеха, технологический маршрут деталей, масса деталей типа «трубка ВВТ».
В ходе проведения компьютерного моделирования была получена укрупненная Парето-оптимальная компоновка участка цеха, где все станки расположены по ходу технологического процесса - это так называемая ^-образная ячейка (рис. 1).
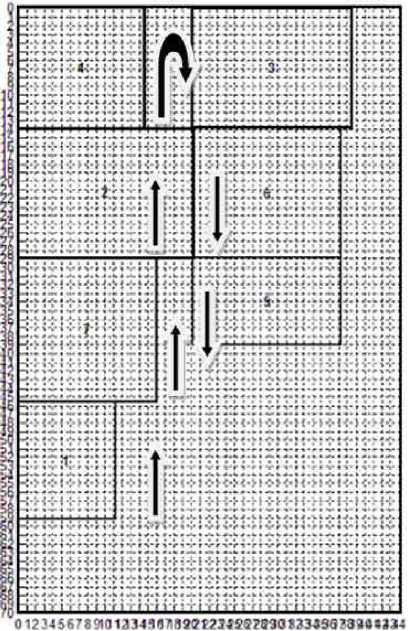
Рис. 1. Укрупненный Парето-оптимальный вариант планировки оборудования
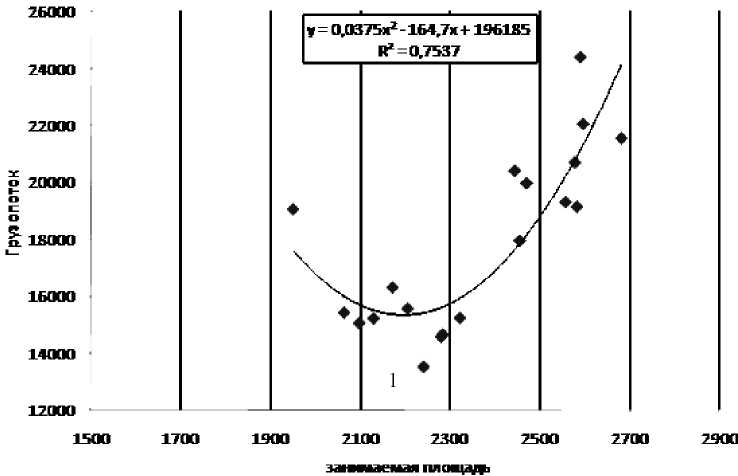
Рис. 2. Зависимость грузопотока от площади (у - соответствует G, а х - величине F)
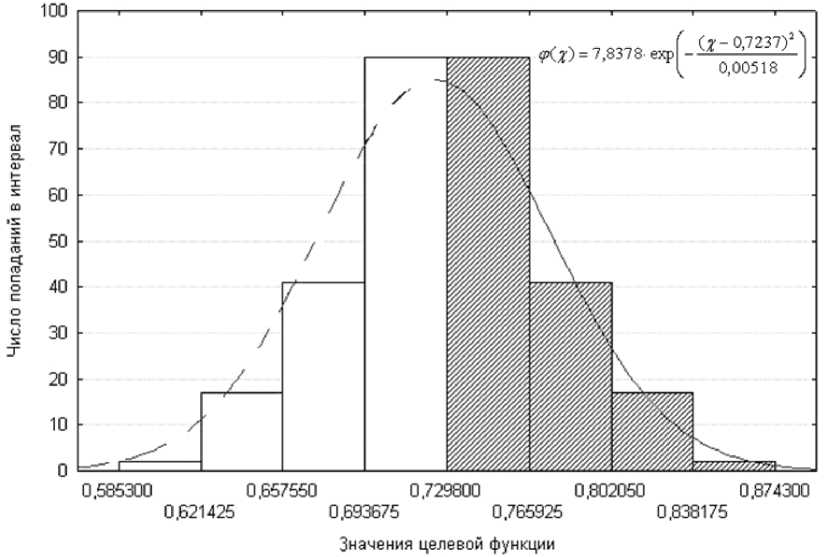
Рис. 3. Усеченный закон нормального распределения значений целевой функции (1) (X - значения целевой функции) при ограничении интервала [0,729;0,8743]
Полученная планировка оборудования соответствует таким основным требованиям, как выполнение принципов прямоточности, минимизация грузооборота, наилучшее использование площадей. В результате укрупненная Паре-то-оптимальная планировка позволяет сократить площадь, занимаемую участком (оборудованием), и минимизировать грузопоток, также из рис.1 видно, что перемещение деталей происходит по ходу маршрутного технологического процесса изготовления изделия-представителя группы.
Для решения задачи многокритериальной оптимизации была также установлена зависимость грузопотока (G) от занимаемой площади (F) (рис. 2). Из рисунка видно, что при минимальной величине грузопотока величина площади не достигает своего минимума. Такая ситуация является классической при использовании методов многокритериальной оптимизации. Отсюда полученная зависимость позволяет определить Парето-оптимальные планировочные решения в рамках использованного выше генетического алгоритма.
В процессе компьютерного моделирования и оптимизации планировок оборудования также было установлено, что значения целевой функции (1) распределяются по усеченному нормальному закону распределения (рис. 3), где максимальная вероятность появлений Парето-оптимальной планировки оборудования приходится на минимальное значение целевой функции, соответствующее точке 1 (рис. 2). При этом на следующем рисунке (рис. 3) видно, что генетический алгоритм относится к «мягким вычислениям», а полученное Парето-оптимальное решение относится к наиболее вероятной планировке оборудования.
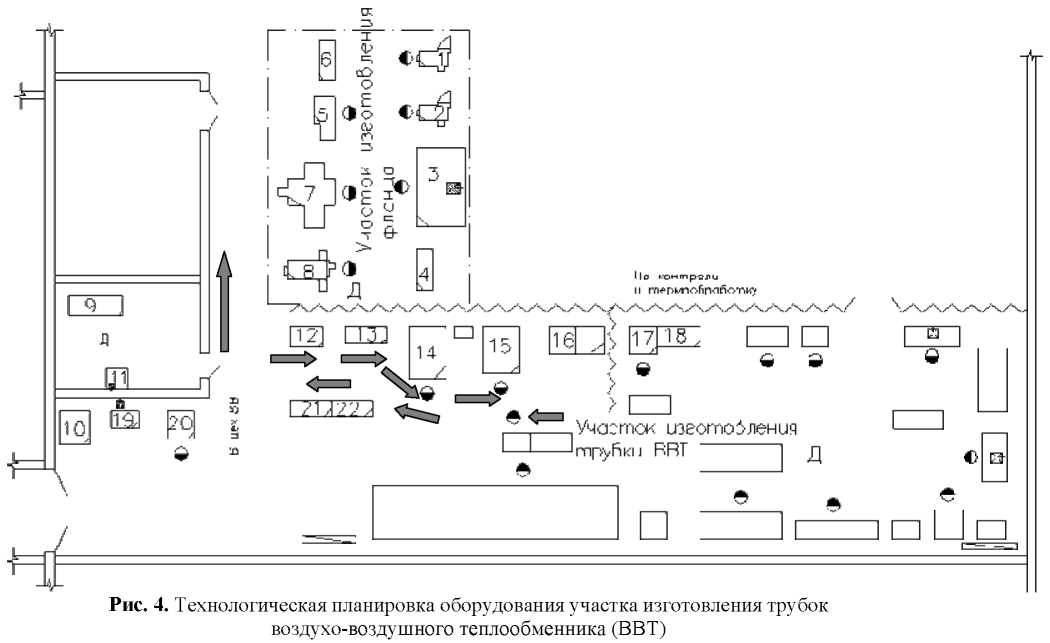
На основании многокритериальной двухшаговой оптимизации с использованием логикогенетического метода можно выполнять исполнительные чертежи технологических планировок оборудования (рис. 4 повернуто относительно осей рис. 1), которые используют для монтажа оборудования цехов «бережливого производства».
Заключение
Использование методов математического моделирования и оптимизации технологических планировок оборудования производственных цехов бережливого производства относится к наиболее актуальным задачам организации «бережливого производства» в машиностроении.
В условиях «бережливого производства» (при формировании потока или технологического маршрута изготовления изделий) необходимо реорганизовывать многие производственные подразделения на основе оптимизации планировок оборудования, минимизирующих грузопоток (G) и производственные площади (F). Таким образом, известные методы искусственного интеллекта для оптимизации размещения оборудования по одному критерию - минимума грузопотока, например, с помощью искусственной нейронной сети Хопфилда или с помощью генетического алгоритма однокритериальной оптимизации, не отвечают всем требованиям оптимизации цехов бережливого производства.
Разработанный в данном исследовании метод укрупненного математического моделирования с использованием генетического алгоритма многокритериальной оптимизации позволяет получать Парето-оптимальные планировки участков цехов «бережливого производства», что подтверждено как теоретическими обоснованиями, так и практическими разработками.
Список литературы
- Вумек Джеймс П., Джонс Дэниел Т. Бережливое производство: Как избавиться от потерь и добиться процветания вашей компании. М.: Альпина Бизнес Букс, 2004. 473 с.
- Лобуз В. В. Формирование технологически ориентированных структур оборудования в пространстве цеха с использованием генетических алгоритмов // Справочник. Инженерный журнал. 2007. № 9. С. 40-46.
- Рутковская Д., Пилиньский М., Рутков-ский Л. Нейронные сети, генетический алгоритмы и нечеткие системы. М.: Горячая линия - Телеком, 2006. 452 с.
- Подиновский В. В., Ногин В. Д. Парето оптимальные решения многокритериальных задач. М.: Наука, 1982. 344 с.
- Селиванов С. Г., Иванова М. В. Теоретические основы реконструкции машиностроительного производства. Уфа: Гилем, 2001. 310 с.
